
Graphs can represent biological networks at the molecular, protein, or species level. An important query is to find all matches of a pattern graph to a target graph. Accomplishing this is inherently difficult (NP-complete) and the efficiency of heuristic algorithms for the problem may depend upon the input graphs. The common aim of existing algorithms is to eliminate unsuccessful mappings as early as and as inexpensively as possible.
We propose a new subgraph isomorphism algorithm which applies a search strategy to significantly reduce the search space without using any complex pruning rules or domain reduction procedures. We compare our method with the most recent and efficient subgraph isomorphism algorithms (VFlib, LAD, and our C++ implementation of FocusSearch which was originally distributed in Modula2) on synthetic, molecules, and interaction networks data. We show a significant reduction in the running time of our approach compared with these other excellent methods and show that our algorithm scales well as memory demands increase.
Subgraph isomorphism algorithms are intensively used by biochemical tools. Our analysis gives a comprehensive comparison of different software approaches to subgraph isomorphism highlighting their weaknesses and strengths. This will help researchers make a rational choice among methods depending on their application. We also distribute an open-source package including our system and our own C++ implementation of FocusSearch together with all the used datasets (http://ferrolab.dmi.unict.it/ri.html). In future work, our findings may be extended to approximate subgraph isomorphism algorithms.

Complex biological systems arise from the interaction and cooperation of a large number of molecular or organismal components. Understanding such systems has required, just at the molecular level, the construction and analysis of protein−protein interaction, metabolic interaction, transcription factor binding, and hormone signaling networks. Networks are represented by graphs, where vertices are, for example, molecular components and edges represent some relationship among them. Understanding such networks mainly requires finding specific topological subgraphs, which entails the application of subgraph isomorphism algorithms [1–3]. Such subgraphs are sometimes called network motifs [4]. These motifs, which could be repeated in the same network or in different networks, give insight into evolutionary mechanisms (analogous to the process of establishing the evolution of proteins through local alignments of sequences). In [5, 6], the authors find network motifs through the following steps: (i) enumerate all possible subgraphs of the network; (ii) classify them in classes of isomorphic subgraphs; (iii) generate random graphs and enumerate and classify all subgraphs in such graphs (i.e. null hypothesis construction); and (iv) establish as motifs all subgraphs classes that appear with higher frequency in the real network than in the random networks. The second step is repeated many times in real and random networks and entails the usage of subgraph isomorphism algorithms [1]. In [7], the authors provides a Cytoscape plugin to query networks by drawing and searching known or user-defined subgraphs. It uses the subgraph isomorphism algorithm of [3]. The authors in [3] and related publications show their speed-up compared to the algorithm in [1] which is used in [5, 6]. In another application, molecular components, such as small or large proteins, are represented as graphs. In such chemical networks, vertices are atoms and edges are the bonds among them. Systems such as Daylight [8] and its academic version Frowns [9], collect a set of molecules represented in two dimensions. Then, given a subgraph, they apply a subgraph isomorphism algorithm [3] to determine how many times and where the subgraphs occur in each molecule of the collection. The aim of the above works is to predict or increase the functionality of new or known molecules. In [10], graphs are used to represent proteins in three dimensions. There, vertices and bonds are associated with their positions in space or contact maps are used. Contact maps represent protein residues and the cut-off distances among them starting from a three dimensional protein structure. The authors discuss subgraph isomorphism algorithms, graph theoretical properties and the importance of an efficient implementation of such algorithms with the aim of detecting ligands that bind to proteins (i.e., common regions in the maps). Finally, in [11], the authors describe the relations among the components and subcomponents of molecules by using hierarchical graphs and making use of subgraph isomorphism algorithms [1] to find common substructures.
Finding a solution for the subgraph isomorphism problem is inherently hard [12] and therefore the efficiency of any software using subgraph isomorphism algorithms largely depends on (i) finding efficient heuristics to make the isomorphism algorithms faster; (ii) reducing the number of subgraph isomorphism calls; and (sometimes) (iii) relaxing the isomorphism conditions.
Graph indexing based methods aim to design efficient indexes (i.e. extracted from graph subgraph, trees or paths [13–18]) or data structures [19, 20] capable of limiting the execution of subgraph isomorphism to only a few candidate graphs; graph mining algorithms [21–24] reduce the size of indices by identifying frequent subgraphs having at least a specified support; and graph pattern matching algorithms [25–28] solve a "near" subgraph isomorphism problem by applying more relaxed reachability conditions [27].
This paper introduces a new algorithm for the subgraph isomorphism problem and compares it on synthetic and biochemical data with the most efficient and recent algorithms present in literature [3, 29, 30]. Notions, concepts and related work are given next.
A graph G is a pair (V, E), where V is the set of vertices and E ⊆ (V × V ) is the set of edges. Let A be a set of labels, the functions lab : V → A and β : E → A assign labels to vertices and edges, respectively. If (u, v) ∈ E, v is called a neighbor of u. Given G, |V | (|E|) indicates the number of vertices (edges). A graph G is dense when the ratio |E|/|V| is high, sparse otherwise.
Given a pattern graph G and a target graph G', the problem is to find an injective function, M : V → V', mapping each vertex of G to a unique vertex of G' such that the following isomorphism conditions are satisfied: if (u, v) is an edge in G, u has label lab(u), v has lab(v), then the corresponding edge (u', v') in G' has lab(u) = lab(u'), lab(v) = lab(v'), and β(u, v) = β(u', v'). Note that there may be an edge (u', v') is ∈ E' without any corresponding edge in E; when this happens, the subgraph isomorphism is also called a monomorphism. When G has exactly the edges that appear in G' over the same vertex set, then G is an induced subgraph of G'.
In what follows, we view G and G' as connected graphs and ignore edge labels (edge labels improve efficiency, because they add more constraints, but complicate the algorithm needlessly). Moreover, we consider graphs that are directed, that is (u, v) ∈ E does not imply that (v, u) is also in E. Our approach applies as well directly to undirected connected graphs. When needed, we denote an undirected edge with 〈u, v〉.
A simple enumeration algorithm to find all the subgraph isomorphisms (i.e., occurrences) of a pattern graph in a target graph works as follows: generate all possible maps between the vertices of the two graphs and check whether any generated map is a subgraph isomorphism (which we will call a match). Whereas this algorithm is inefficient if done naively, it serves as a good starting point.
All the maps can be represented using a search space tree. The tree has a dummy root. Each node represents a possible match between some vertex u of the pattern G and some vertex u' of the target graph G' . The path from the root to a given node represents a partial match between G and G' . Only certain leaves correspond to subgraph isomorphisms between the pattern and the target graph (see Figure 1 for an example of a search space tree). During the visit, the isomorphism conditions are applied to verify the partial matches. When the conditions are not satisfied the algorithm prunes the underling branches and backtracks on the parent nodes of the search tree. The size of the above search space tree increases exponentially with the graph size. Because the subgraph isomorphism problem is NP-complete [12] (to be precise, subgraph isomorphism of graphs with repeated labels or no labels is an NP-complete problem; such graphs are typical in biomedical applications) a cheaper-than-exponential algorithm may not exist. Next we sketch the main heuristics in existing subgraph isomorphism algorithms. The common aim is to eliminate unsuccessful mappings as early as possible.
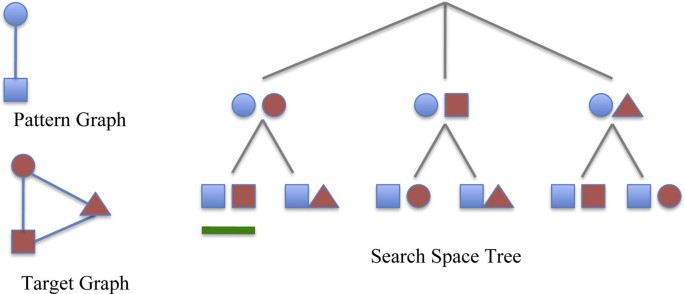
Search strategy An important factor influencing an algorithm's performance is the choice of a good variable ordering (sometimes called a search strategy) of the pattern graph vertices in the branches of the search tree. For example, a variable ordering may begin with a pattern vertex having the highest degree or having the most uncommon label in the target graph [31, 32]. A strategy depending on the partial solution could choose the next pattern vertex to be matched such that the number of children in the current search tree's branch is minimized [29]. One can choose to maintain the same variable ordering for all the branches of the search tree or can choose different orderings for different branches. These two strategies are called static ordering and dynamic ordering [29, 33], respectively.
An important difference between static and dynamic orderings is that the first one can be chosen a priori, before the search phase. Dynamic strategies must be elaborated during the search.
Reduce the search space After evaluating a partial solution, an algorithm may backtrack if there is no possible mapping for the remaining unmatched vertices [3]. Alternatively inference-based techniques can predict future branching of the search tree thus avoiding the need to explore partial solutions that do not result in a match [29, 30]. An intelligent matching algorithm orders vertices well and filters well. However, intelligence often comes at a cost.
Next, we briefly describe the state of the art. We refer to [3, 29, 30, 34] for a deep treatment of the subject.
A popular algorithm, VFlib, was presented by Cordella et al. in [3]. It uses a dynamic search strategy. Given a partial solution, first it chooses unmatched pattern vertices having edges starting from vertices in the partial solution; then it chooses those unmatched vertices having edges ending in vertices in the partial solution. In order to reduce the search space, the approach uses the following two lookahead heuristics. A mapping pair (u, u'), where u and u' are vertices of the pattern and target graph, respectively, is considered a valid match if it satisfies the following rules: (i) u and u' are both neighbors of matched vertices; (ii) the number of unmatched pattern vertices which are neighbors of matched vertices and are connected with u must be less than or equal to the number of unmatched target vertices which are neighbors of matched vertices and are connected with u'; (iii) the number of vertices connected with u and not in (i) and (ii) must be less than or equal to the number of vertices connected to u' that are not in (i) or (ii). The rule (ii) is subdivided into four cases depending on the direction of involved edges between the neighbors of u and the set at (i).The rule (iii) applies only for induced subgraph isomorphism as opposed to monomorphisms.
Subgraph isomorphism may be modeled as a constraint satisfaction problem (CSP). Given a set of variables (pattern vertices) and a set of constraints among them, a solution of a CSP for the subgraph isomorphism problem consists of finding an assignment of values (target vertices) to all variables such that all constraints are satisfied. Initially, each pattern variable v is associated with a set of values formed by the set of target vertices that could be matched to v, i.e. lab(v) = lab(M(v)) and the degree of v is less of degree of M(v). That set is called the domain of v. Constraints guarantee that isomorphism conditions are maintained.
Several filtering techniques, such as forward-checking [34], prune the branches of the search tree by propagating constraints to remove values from potential domains (i.e., domains of variables not yet assigned).
A branch is pruned when a domain becomes empty. In forward checking, first a variable is assigned, then all constraints involving such variables are propagated to remove values from other domains that are not consistent with the current assignment. This is called inference.
Solnon in [30] proposes LAD, which combines the constraints that two pattern vertices cannot be matched with the same target vertex into a partial solution, together with the preservation of edge correspondence between the pattern graph and the target graph. Such constraints are applied during backtracking and are propagated until convergence (i.e., as much as possible). LAD defines a dynamic search strategy where the next pattern vertex to be assigned is the vertex with the smallest domain cardinality.
Recently, Ullmann proposed an algorithm called FocusSearch [29]. The search process is done by a backtracking algorithm that applies a bit-vector domain reduction to each step. Before the search starts, it runs two preliminary steps. The first one, called prematch, fills domains by filtering them using vertex invariants based on labels and topology. The second one locally ensures that two pattern vertices cannot be matched to the same target vertex. After the preliminary steps, a static search strategy orders the pattern vertices in the following way: each pattern vertex with a single compatible target vertex is put at the head of the sequence and the next pattern vertex to be matched is the one with the highest number of branches between it and the partial solution. If there are two vertices that are equal candidates to be the the next vertex in the ordering, it chooses the one with the highest sum of the degrees of its neighbors.
Other methods in the literatures do not rely on backtracking or CSP techniques, but rather apply heuristics based on probabilistic functions, explicit enumeration of matches, and so on [35–46].
Inference-based methods, which propagate constraints until convergence (for example LAD), reduce the search time to the greatest extent. Unfortunately, such inference is done at the price of a greater computational cost. On the other hand, when constraint verification is applied only locally (for example, the local inference used by FocusSearch and the pruning rules of VFlib), it is crucial to define a search strategy that tries to prune the search space as much and as early as possible at low cost. This aspect is not addressed by VFLib. FocusSearch applies this concept only partially. It defines a static and partly target-dependent search strategy reflecting the pattern topology. It also performs local inference, minimizing the cost by using bit-vectors. In this paper we present a novel subgraph isomorphism algorithm, called RI (http://ferrolab.dmi.unict.it/ri.html). It creates a search strategy based only on the pattern graph topology. The order is chosen to create constraints as early as possible in the matching phase. Roughly, vertices having high valence and that are highly connected with vertices previously present in the ordering tend to come early in the final variable-ordering. During the matching phase, RI does not apply any computationally costly pruning or inference rules. This is the first paper that compares all the most recent and used algorithms (LAD, FocusSearch, VFlib). We analyze algorithmic aspects including the size of search space, the memory requirement, the timeout of the algorithms, the matching time and the total time, varying the density and dimension of pattern and target graphs, the number and the distribution of the labels. Dataset characteristics are typical of molecular biological data. We also used the synthetic data analyzed in the previous work by authors of LAD and VFLib. In order to validate our strategy, we compare RI and two versions of RI, called RI-Ds and RI-DsPm. RI-Ds computes, after defining the variable order of pattern vertices and before the subgraph isomorphism starts, an initial domain assignment. For each pattern vertex, RI-Ds computes its domain and verifies that pattern edges are compatible in the target domains. It does not apply inference or domain reduction during backtracking. This low-priced verification helps in large dense targets, because it reduces the number of candidates to be verified during backtracking. RI-DsPm, in addition to RI-Ds, uses the prematch phase defined in FocusSearch, i.e. filters domains by using vertex invariants based on neighbor labels and topology. We show that RI-DsPm does not improve performance compare to RI and RI-Ds. This behavior is supported by the analysis given in [29] (see in [29] Section 7.7 "Molecular graph retrieval experiments"). Moreover, it validates the main ideas in RI: a powerful pattern vertex ordering, i.e. strongly dependent only on pattern graph topology, together with light constraint verification, is more efficient than a local or global inference procedure.
Compared software We compared RI, along with variants RI-Ds and RI-DsPm with VFlib (using the last released version named VF2), LAD and FocusSearch measuring the search space size, the matching time, the memory requirements and the total time.
RI, RI-Ds, RI-DsPm, VF2 and LAD are implemented in C/C++. Since FocusSearch has been released in Modula2, in order to compare the algorithms under the same platform, we re-implemented FocusSearch in C++ following the author's guidance and the original source code.
Next we describe the pattern and target graphs used to test the algorithms. Table 1 reports the statistics on the number of vertices, edges and labels of the real target graphs described below. We refer to the Additional File 1 for details on the synthetic datasets. We consider all graphs to be directed. We transform undirected graphs into directed graphs by replacing each edge connecting two vertices with two edges.

The scores are assigned in the following way. Let m be the next step of a visit in the pattern graph and let μ (u0, u1, . um−1) the visited vertices so far. Let u m be the next candidate vertex to be inserted in μ.
We can ascribe a score to u m using the following three sets.
The score of candidate u m is a lexicographic score based on |V m,vis | as the high order quantity, followed by |V m,neig | and finally |V m,unv |. Thus, suppose u a and u b are both candidates. The score of u a is greater than the score of u b if either (i) |V a,vis | >|V b,vis | or (ii) |V a,vis | = |V b,vis | and |V a,neig | >|V b,neig | or (iii) |V a,vis | = |V b,vis | and |V a,neig | = |V b,neig | and |V a,unv | >|V b,unv |. If two vertices tie for the highest score, then we choose one arbitrarily and keep track of the other.
Note that, if we are working with directed graphs then our algorithm increases the score more when both underlying directed edges are present than if only one of the pair exists.
Figure 3 reports an example of the RI search strategy. The first vertex inserted in μ is 4, since it has the highest number of edges. Then, suppose that μ = , the candidates to be inserted are vertices 0,2,6,5 and 7. The next vertex that will be inserted in μ is 5. The reason is that, even though it has the same number of edges pointing to vertices in μ as vertex 0, the vertex 5 has a higher number of edges pointing to neighbors of vertices in μ (i.e. point to 2 and 7). Even though the node 5 has fewer edges pointing to all remaining vertices (i.e. consider the edge 〈5, 8〉 for 5, and for 0 the edges 〈0, 3〉 and 〈0, 9〉), this case has less weight in the defined score.
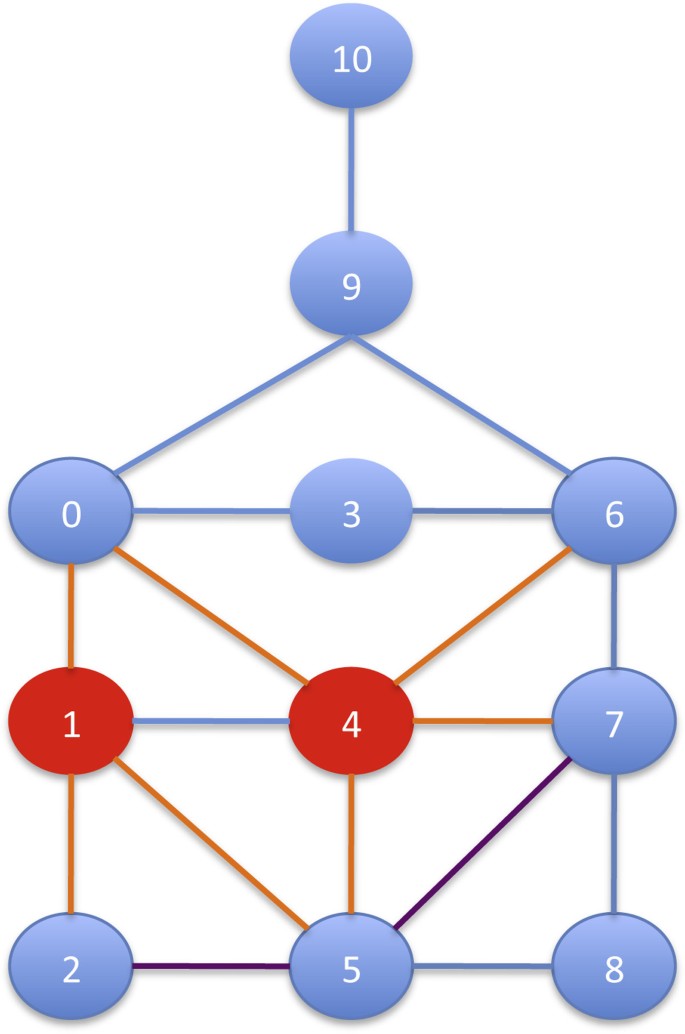
Finally, we point out that our search strategy does not favor (i.e. put in the ordering first) more dense parts of the pattern graph nor the most central vertex according centrality measures such as between centralities and so on. In fact, in the example in Figure 3 the most central vertices 6 and 0 are not at the beginning of the ordering.
Each node in the search space tree represents a mapping from a vertex in the pattern graph to a vertex in the target graph. All paths from the root downward in the tree correspond to the order of vertices μ in the pattern graph generated by GreatestConstraintFirst. The vertices from the pattern graph must be compared to every vertex in the target graph to see whether it satisfies the subgraph isomorphism conditions. Each step consists of choosing, at each level i, the candidate vertices in the target graph, u i ′ = M u i to match u i , among the neighbors of the matched vertices of the parents of u i . Parents of the pattern graph are constructed in GreatestConstraintFirst. The following isomorphism conditions prune away un-feasible paths.
The isomorphism conditions are tested in the above. Condition i is verified only if condition i − 1 does not fail. Conditions 1, 2, and 4 ensure the isomorphism, whereas the third one is a filtering test that often obviates the need for the substantial work needed to verify condition 4. The above matching procedure, called Matching, is illustrated in Figure 4.

RI is the first to suggest a static and target independent search strategy. It reduces the search space by applying only the subgraph isomorphism conditions rather than costly filtering rules as in [3] or inference procedures as in [2, 29, 30]. It's not a priori clear that this will be better. Inference or pruning rules that look at the target graph and that consider the actually partial solutions can reduce the space search more, but may be more expensive.
VFlib [3] and LAD [30] define a dynamic search strategy that looks at the target graph; FocusSearch [29] defines a partly dynamic search strategy, almost independent from the target graph. FocusSearch first looks at the target graph to run a domain reduction by filtering them using vertex invariants based on labels and topology. This is used to select the first vertex of the variable ordering. Then it constructs the rest of the sequence of vertices by applying topology constraints only on the pattern graph. FocusSearch has less pruning power than LAD, but the overhead is also less.
Besides the fact that RI is static, the rules are different too. For example, (i) in contrast to VFlib rules, RI does not distinguish among edges going out or into a vertex, (ii) FocusSearch can handle only integer label edges, and (iii) LAD cannot perform induced subgraph isomorphism and cannot deal with edge labels. Table 2 summarizes the main differences among RI, VFlib and FocusSearch.
Table 2 Comparison of subgraph isomorphism algorithms.This article is published as part of a supplement. The publication costs for this article were funded by PO grant - FESR 2007-2013 Linea di intervento 4.1.1.2, CUP G23F11000840004.
We would like to thank the authors of VFlib, LAD and FocusSearch for having kindly provided their tools for comparison purpose. In particular, we thank J. R. Ullmann for very informative discussions.
This article has been published as part of BMC Bioinformatics Volume 14 Supplement 7, 2013: Italian Society of Bioinformatics (BITS): Annual Meeting 2012. The full contents of the supplement are available online at http://www.biomedcentral.com/bmcbioinformatics/supplements/14/S7